Category: Artifact

Posted on

SOME MATHEMATICAL THEOREMS ON PERSPECTIVE DRAWING

From: Chapter 10, Mathematics for the Nonmathematician, Morris Kline

Let us accept, then, the principle that the canvas must contain the same section that a glass screen placed between the eye of the painter and the actual scene would contain. Since the artist cannot look through his canvas at the actual scene and may even be painting an imaginary scene, he must have theorems which tell him how to place his objects on the canvas so that the painting will, in effect, contain the section made by a glass screen.

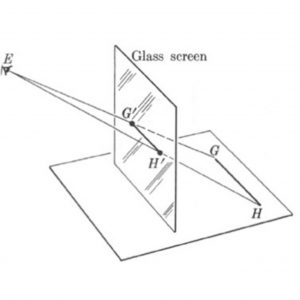
Suppose then that the eye at E (Fig. 10–8) looks at the horizontal line GH and that GH is parallel to a vertical glass screen. The lines from E to the points of GH lie in one plane, namely the plane determined by the point E and the line GH, for a point and a line determine a plane. This plane will cut the screen in a line, G′H′, because two planes which meet at all meet in a line. It is apparent that the line G′H′ must also be horizontal, but we can prove this fact and so be certain. We can imagine a vertical plane through GH. Since GH is parallel to the screen and the latter is also vertical, the two planes must be parallel. The plane determined by E and GH cuts these parallel planes, and a plane which intersects two parallel planes intersects them in parallel lines. Hence G′H′ is parallel to GH, and since GH is horizontal, so is G′H′. But GH was any horizontal line parallel to the screen. Hence the image on the screen of any horizontal line parallel to the screen or picture plane must be horizontal. Thus in a painting which is to contain what this glass screen contains, the line G′H′ must be drawn horizontally.

We can present practically the same argument to show that the image of any vertical line, which is automatically parallel to the vertical screen, must appear on the screen as a vertical line. Thus all vertical lines must be drawn vertically. Continue reading “SOME MATHEMATICAL THEOREMS ON PERSPECTIVE DRAWING”

Posted on

Dorje

True view is infinite and vast. 
Relax and release mind of thought.
Shatter that which arises, 
        with “p-hat!”
Transparent and clear at last, 
Recognize pure awareness sought,
Without notion such this or that. 

Meditate on rays of love and wisdom,
Rest in awareness beyond description. 
Abide by flow of primordial glow.
Decide with conviction absolute,
On one thing and one thing only, resolute. 

In action as the compassionate one, 
Momentary thoughts leave no trace, 
Like writing on ocean’s surface.
Arising and liberation become
natural and continuous cure,
Without trace and innately pure. 
With confidence in liberation of rising thoughts, succumb. 

For view is of three part in communion, 
Meditation is wisdom and love in union
Accompanied by action of compassion. 

(A reflective render on The Special Teaching of the Wise and Glorious King)
Posted on

A BASIC MEDITATION

Credit: John Myrdhin Reynolds (www.vajranatha.com/)

BASIC MEDITATION PRACTICE

The first thing we need to discover in meditation practice is something called mindfulness or mindful awareness. This is basic. Mindfulness is an awareness that is present together with our immediate experience, whether sensations, thoughts, or emotions. This awareness is not distracted or caught up in any secondary mental processes, but remains at the primary level of immediate experience.

The first exercise is called “mindfulness on breathing”. First sit down comfortably, on a cushion on the floor or on a chair, but making sure that the back is straight. This harmonizes the flow of psychic energy in the body. We will be sitting still and unmoving for a time. This is the opposite of our usual everyday habit of running around and being distracted. Relax and do some deep breathing in order to release stress and tension. But here we have relaxation with alertness, which is the opposite of being sleepy, drowsy, and dull. We are alert and fully awake. But sitting calmly and quietly.

We are not thinking about anything, but are open and globally aware. This is not absorption or trance or withdrawal of the senses. The senses are open and operating fully. This is what is meant by “clarity”. We ground and center ourselves just where we are in our immediate experience. Just be here now. This is like a tree, just being. It is nothing special. It is just sitting and being centered. It is not doing anything special. We are alert and aware without distractions. Distractions are what move us off center. They take us on a trip and we forget who and where we are. This just being present and aware is what is called mindfulness.

The ‘classical’ Buddhist exercise for mindfulness is fourfold: there is mindfulness on bodily sensations, mindfulness on feelings and emotions, mindfulness on thoughts, and mindfulness of subliminal processes. Mindfulness is just being present. It is self-remembering, a remembering to be aware, a coming back to center again and again. It is necessary first to develop this mindful presence so that we can engage in self-observation or introspection. We can be easily distracted; that is our habit and we continuously impose our conceptions on what we experience. So, it is necessary to have a focus for our awareness.

In this case, we begin with the physical body and focus our attention and our full concentration on our breathing, just the sensations and sounds of our breathing. Breathing is part of our entire dimension of energy. Breathing links our body and our mind. It is a system that is both automatic and voluntary. In this case, we are just breathing normally with our eyes closed and sitting quietly. We simply focus on our breathing. If we become distracted or if thoughts arise, simply come back to focusing on our breathing. Just watch this breathing, be in this breathing. We are not thinking about our breathing or judging it. We just let it be without elaborations. This is known as Anuprana-smriti, practicing mindfulness again and again on our breathing. In this way, we can discover our awareness.

Posted on

Item six on the agenda….

From "Monty Python's The Meaning of Life" (1983 Film)

CHAIRMAN: ...Which brings us once again to the urgent realization of just how much there is still left to own. Item six on the agenda: the meaning of life. Now, uh, Harry, you've had some thoughts on this.

HARRY: That's right. Yeah, I've had a team working on this over the past few weeks, and, uh, what we've come up with can be reduced to two fundamental concepts. One: people are not wearing enough hats. Two: matter is energy. In the universe, there are many energy fields which we cannot normally perceive. Some energies have a spiritual source which act upon a person's soul. However, this soul does not exist ab initio, as orthodox Christianity teaches. It has to be brought into existence by a process of guided self-observation. However, this is rarely achieved, owing to man's unique ability to be distracted from spiritual matters by everyday trivia.
[pause]

BERT: What was that about hats, again?
“Galaxy Song”song by Eric Idle From “Monty Python’s The Meaning of Life“ 
“Galaxy Song”
 by Eric Idle (lyrics) and John Du Prez (music)

Whenever life gets you down, Mrs. Brown,
And things seem hard or tough,

And people are stupid, obnoxious, or daft,
And you feel that you've had quite enough,

Just remember that you're standing on a planet that's evolving
And revolving at nine hundred miles an hour,
That's orbiting at nineteen miles a second, so it's reckoned,
A sun that is the source of all our power.
The sun and you and me and all the stars that we can see
Are moving at a million miles a day
In an outer spiral arm, at forty thousand miles an hour,
Of the galaxy we call the 'Milky Way'.

Our galaxy itself contains a hundred billion stars.
It's a hundred thousand light years side to side.
It bulges in the middle, sixteen thousand light years thick,
But out by us, it's just three thousand light years wide.
We're thirty thousand light years from galactic central point.
We go 'round every two hundred million years,
And our galaxy is only one of millions of billions
In this amazing and expanding universe.

The universe itself keeps on expanding and expanding
In all of the directions it can whizz
As fast as it can go, at the speed of light, you know,
Twelve million miles a minute, and that's the fastest speed there is.
So remember, when you're feeling very small and insecure,
How amazingly unlikely is your birth,
And pray that there's intelligent life somewhere up in space,
'Cause there's bugger all down here on Earth.
“The Crimson Permanent Assurance” (1983)
Posted on

Without

Without suffering,
  no salvation to be won. 
Without adversity, 
  nothing to overcome. 

With nothing to surrender
  difficult to render realization
  of impermanence, 
  which leads to an awareness 
  of inherit emptiness, 
The awareness, 
  of  self-liberation. 

If on fire would one not extinguish? 
What does one do when hungry?
When tired and sleepy? 
When cold and fire burns low? 

In pain, seek relief, 
  when sick the cure. 
Before a reaping one must sow.
Posted on

Where I

Ponderously Planting trees,
Whose prospective shade
In full bloom will not shelter me,
who aspires for whom,
If all, even “I” are empty?

The guide to land of milk and honey
Promised they who followed,
Tribes that once worshiped hollows, 
Over countless dunes of sand,
There they'd find the promised holy land,
Consecrated by where would stand
No man but son of man.

For on the tribal pyre,
Burns liberties fire. 

Ponderously Planting trees,
Who and whom would free,
If all by self are freed?