From: Chapter 10, Mathematics for the Nonmathematician, Morris Kline
Let us accept, then, the principle that the canvas must contain the same section that a glass screen placed between the eye of the painter and the actual scene would contain. Since the artist cannot look through his canvas at the actual scene and may even be painting an imaginary scene, he must have theorems which tell him how to place his objects on the canvas so that the painting will, in effect, contain the section made by a glass screen.
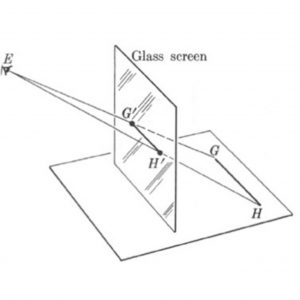
Suppose then that the eye at E (Fig. 10–8) looks at the horizontal line GH and that GH is parallel to a vertical glass screen. The lines from E to the points of GH lie in one plane, namely the plane determined by the point E and the line GH, for a point and a line determine a plane. This plane will cut the screen in a line, G′H′, because two planes which meet at all meet in a line. It is apparent that the line G′H′ must also be horizontal, but we can prove this fact and so be certain. We can imagine a vertical plane through GH. Since GH is parallel to the screen and the latter is also vertical, the two planes must be parallel. The plane determined by E and GH cuts these parallel planes, and a plane which intersects two parallel planes intersects them in parallel lines. Hence G′H′ is parallel to GH, and since GH is horizontal, so is G′H′. But GH was any horizontal line parallel to the screen. Hence the image on the screen of any horizontal line parallel to the screen or picture plane must be horizontal. Thus in a painting which is to contain what this glass screen contains, the line G′H′ must be drawn horizontally.
We can present practically the same argument to show that the image of any vertical line, which is automatically parallel to the vertical screen, must appear on the screen as a vertical line. Thus all vertical lines must be drawn vertically.
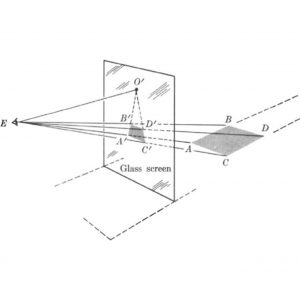
Now let us consider a somewhat more complicated situation. Suppose that AB and CD (Fig. 10–9) are two parallel, horizontal lines in an actual scene. Moreover, assume that these lines are perpendicular to the screen. The eye is at E. If we now imagine that lines go from E to each point of AB, these lines, that is the projection, will lie in one plane for the point E, and the line AB will determine this plane by virtue of the theorem of solid geometry already mentioned. Similarly, E and the line CD determine another plane. The screen cuts the two planes we have just described; The sections must lie on the screen, and our problem is to determine where they should lie.
Of course, the intersection of two planes is a line, and so the section corresponding to AB and that corresponding to CD will be lines, A′B′ and C′D′, respectively. Moreover, as the eye at E looks farther and farther out along the parallels AB and CD, the lines of sight will become more and more horizontal. As the eye follows AB and CD to infinity, so to speak, the lines from E tend to merge into one horizontal line which will be parallel to AB and CD. This line from E will pierce the screen at some point, say O′, and this point corresponds to the imaginary point O where AB and CD seem to meet at infinity. Of course, AB and CD are parallel and do not meet, but it is convenient to think of them as meeting at a point at infinity. Indeed, the eye gets the impression that they do meet. Then the line EO′ will be perpendicular to the screen because it is parallel to AB and CD and these two lines are perpendicular to the screen. The point O′ corresponds to the imagined meeting point at infinity of AB and CD, but because this point does not actually exist, O′ is called the principal vanishing point. It vanishes in the sense that it does not correspond to any actual point on AB or CD, whereas other points on A′B′ or CD′ do correspond to actual points on AB or CD, respectively.
Now the lines AB and CD extend out to infinity to the hypothetical meeting point O; that is, ABO and CDO are lines in the real scene. The sections of these lines, A′B′O′ and C′D′O′, must therefore meet at O′. What we have shown then is that A′B′ and C′D′ must be placed on the screen so that they meet at O′, and O′ is the foot of the perpendicular extending from the eye to the screen. Let us now note that AB and CD are any horizontal lines perpendicular to the screen. Hence all horizontal lines which are perpendicular to the screen must be drawn so as to go through O′, the principal vanishing point, which is the foot of the perpendicular from the eye to the screen.
We may draw another important conclusion from the preceding situation. The distances AC and BD are equal, for they are the distances between parallel lines. However, the corresponding images A′C′ and B′D′ are not equal because the lines A′B′ and C′D′ converge to O′. Moreover, B′D′ will be shorter than A′C′ because it is closer to O′. But B′D′ corresponds to the actual distance BD which is farther from the screen than AC is. Hence lengths which are farther from the screen must be drawn shorter than equal lengths closer to the screen. This fact is often described by the statement that, to obtain proper perspective in a painting, lengths farther away from the observer must be foreshortened.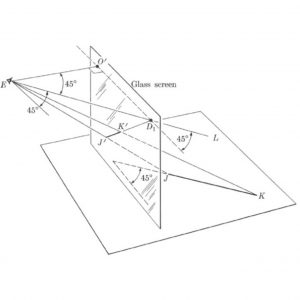
We shall establish one more theorem about perspective drawing. Let us now suppose that JK (Fig. 10–10) is a horizontal line which makes an angle of 45° with the screen. Assume that the eye at E looks out along the line JK toward infinity. Then the line from the eye to the point at infinity on JK will be parallel to JK. Since JK is horizontal, the new line, EL in Fig. 10–10, will also be horizontal. It will pierce the screen at some point, say D1, and will also make an angle of 45° with the screen. The triangle D1EO′ is a right triangle because EO′ is perpendicular to the screen. In view of the acute angles of 45°, O′D1 = EO′. Then the point D1 is as far from O′ as E is. The projection from E to the various points of JK cuts the screen in some line, J′K′, say. As the eye continues to follow JK toward infinity, the projection cuts the screen in points lying on an extension of J′K′, and we have already established that when the eye looks toward infinity on JK, the projection cuts the screen at D1. Hence J′K′ must go through D1. We now have another important result. The image of any horizontal line which makes an angle of 45° with the screen must go through the point D1 which lies on the screen, on the same level as E, but is as far to the right of the principal vanishing point as E is from the principal vanishing point. The point D1 is called a diagonal vanishing point.
Had we considered instead of JK lines which make an angle of 135° with the screen, we would have found that their images must go through a point D2 which lies as far to the left of O′ as E is from O′. The point D2 is also called a diagonal vanishing point.
We see, then, that the points O′, D1 and D2 correspond to points at infinity in the actual scene. As a matter of fact, all points on the horizontal line D2 O′D1 correspond to points at infinity in the actual scene, and this line is called the vanishing line. It is the image of what one might call the horizon in the actual scene, that is, the points at infinity toward which the eye gazes when it looks in a horizontal direction.
The above theorems hardly begin to illustrate what one must know and apply to draw actual scenes realistically. The treatment of curves is especially difficult. For example, actual circles and spheres cannot, in general, be drawn as circles unless their centers happen to lie on the perpendicular from the eye to the screen. In all other cases, they must be drawn as ellipses or as arcs of parabolas or hyperbolas, depending upon their position relative to the observer. This fact becomes clear if one considers that the lines from the eye to each point on the edge of the circle or sphere, the projection, in other words, form a cone and that the section of this cone on the screen will be one of the conic sections discussed in Chapter 6. We shall not investigate the more complicated theorems because to do so would require a course in the subject and because the detailed theorems are of interest only for the specific purpose of learning to paint realistically. We may have seen enough of the basic principles to appreciate that the problem of painting realistically is handled by the application of a thoroughly mathematical system.
We know that the construction of a painting in accordance with the focused scheme presupposes a definite fixed position of the painter in relation to the scene. To view properly a painting so constructed, the observer should place himself in precisely the position the painter used in planning the painting. Otherwise the observer will get a distorted view. Strictly speaking, paintings in museums should be hung so that the observer can conveniently take that position.